ゴルフのスタッツ|STATS
 スタッツ (stats) とは statistics、つまり、「統計」という意味の言葉の略称 (abbreviation) である。しかし、スポーツの世界で スタッツと言えば 選手やチームのプレーの結果を数値化してデータ処理をし、プレーの傾向を分析したり、強み弱みを把握する目的に使うデータであるパフォーマンス・スタッツのことを意味するのが一般的だ。スポーツ中継の解説などでも度々引き合いに出されるものだが、ゴルフでもご多分に漏れず スタッツの話を耳にすることは 珍しくない。
スタッツ (stats) とは statistics、つまり、「統計」という意味の言葉の略称 (abbreviation) である。しかし、スポーツの世界で スタッツと言えば 選手やチームのプレーの結果を数値化してデータ処理をし、プレーの傾向を分析したり、強み弱みを把握する目的に使うデータであるパフォーマンス・スタッツのことを意味するのが一般的だ。スポーツ中継の解説などでも度々引き合いに出されるものだが、ゴルフでもご多分に漏れず スタッツの話を耳にすることは 珍しくない。
♦ パフォーマンス・スタッツ

しかし、これらのデータが 選手の能力を どこまで表しているかは疑問も残る。我々の多くは 平均パット数 (overall putting average) 即ち 1ラウンドに何パットするか を考えて 自分のパッティング能力を評価しようとするが、実は この平均パット数で 本当のパット力を評価しようとしても 無理があるのだ。例えば、寄せの上手な人は パットがあまり上手でなくとも 平均パット数は 低くなるし、その逆も 然りである。そうした観点から PGA や LPGA で パッティング能力の比較は パー・オンしたホールのパット数だけをベースに計算した平均パット数 (putting average) を引き合いに出して 論じるのが慣例だった。例えば、PGA の 2015-2016 シーズンの 2月末時点の overall putting average で トップの選手は 1.50-stroke 前後である。ただし、このスタッツで上位の選手の成績は然程良くない。それに対して、putting average で トップの選手は 1.66-stroke となっているが、このスタッツの上位者は 成績上位の選手が殆どである。いずれにしても、スタッツの見方、使い方は その意味を十分に理解した上で 利用しなければ 価値が半減してしまうと言うことだ。
♦ PGA が採用した新たなスタッツ
近年、PGAでは選手のプレーに関して様々なデータを取るようになった。各選手のティ・ショットから最後にホールアウトするパットまでのデータが全ホールにわたって採取される。それは膨大な量のデータであるが、そうしたデータ処理の能力が飛躍的に伸びたことから、様々な統計データを取ることが可能になった。特定の距離、例えば、10 feet からの全選手の平均パット数を出すことも出来る。同様に、誰が ピンまでどの位の距離のショットで グリーンに乗せたか というようなデータも収集されるから、特定の距離からグリーンに乗ったパーセンテージのようなデータさえ 計算できるのだ。
そこで、2011年から 新たに導入されたのが ストロークス・ゲインド (strokes gained) パッティング 及び ティ・トゥー・グリーン (tee-to-green) という種類のスタッツである。選手のパッティングと ティー・トゥー・グリーンのプレー、つまり パット力とショット力を 出場選手全員の平均値とのストローク差で比較する目的のデータだ。» PGA 説明資料(英語)
先程、average putting の方が overall average putting よりも パッティングの能力を示す指標としては適切だと説明したが、実は、パー・オン率が同じでも、ピンからどの位の距離にパー・オンするかという能力に差があれば、同じパット力の選手でも putting average に差が出てくる訳だから、putting average でも 正しく能力を比較する指標としては 不十分なのである。そこで提案されたのが ストローク・ゲインド・パッティングというスタッツだ。各選手の様々な距離からのパッティング数を(距離別に)全選手の平均パッティング・ストローク数と比べる手法で 1 ラウンドにどれだけパッティングで稼いだか、または、損をしたかを表すことが出来るデータである。これでも 距離と関係のないパットの難易度の要素が考慮されていないから 完全なものとは言えないが average putting より 圧倒的に 理想に近づいたデータになっている。ティー・トゥー・グリーンも 同様に スルーザグリーンのショットで 1ラウンドで どれだけ稼いだか、損をしたかを表すデータである。
因みに、2015-2016 シーズンの 2月末時点の strokes gained putting の 1位の選手は Steve Stricker (1.224)、2位は Jordan Spieth (1.089) である。松山英樹選手は 158位タイ (-0.253)、石川遼選手が 94位 (0.129)。松山選手は パットが悪いのに成績を残しているが、実は strokes gained tee-to-green が 1位 (2.183) なのである。2位は Adam Scott (2.155)、他方、石川選手は 201位 (-1.499) と ショットに課題が見えてくる。この二つのデータを足すと松山選手は 2.183 - 0.253 = 1.930、石川選手は 0.129 - 1.499 = -1.370 という状況。今シーズンの二人の成績の差が その内容も含め 判明する。平均スコアでは 松山選手が 4位、石川選手は 残念ながら 199位である。
♦ ショットのバラつき
さて、統計学は 上述のようなスタッツとは別に コース・マネジメントの観点から極めて有用な使い方が出来るのを ご存じだろうか。自分のショットのバラつきを定性的 また 定量的に 統計学の手法を用いて 分析し、その結果をコース・マネジメントに活用するのである。この後の統計学の基礎で少し詳しく説明するが、ショットの左右へのバラつきは 所謂 正規分布的にバラつくので、その事実に基づいて コース・マネジメントをすれば スコアアップに寄与するという お話しである。
| ショット | 距離 | 左右 |
| #1 | 152 | +6 |
| #2 | 148 | -4 |
| #3 | 144 | -8 |
| #4 | 150 | 0 |
| #5 | 154 | -2 |
| #6 | 140 | +4 |
| #7 | 152 | -10 |
| #8 | 152 | +8 |
| #9 | 146 | +2 |
| #10 | 138 | -14 |
| 平均値 | 147.6 | -1.8 |
| σ | 5.5 | 7.2 |
平均値の解釈については あまり説明を要しないと思うが、σ については説明を要する人が少なくないと思うので 簡単に説明しよう。実は このデータを分析し、σ の数値を見ることで この人のショットのブレについて有意義な推測が可能になるのである。このケースでは まず 95% の確率で 右へのショットのブレは 1.8ヤード + 14.4ヤード (2σ) = 16.2ヤード内、左へのブレは 14.4 - 1.8 = 12.6ヤードの範囲に収まると言うことが推測できるのである。より信頼できるデータを得るためには こうしたデータ取りを 間を置いて 複数回して もっと大きな母集団にして分析をすることだが、いずれにしても、こうしたデータを統計学的に分析することで、コース・マネジメントに有益なデータが得られる訳だ。
こうしたデータがあれば、自分のショットの傾向が統計学的に把握できている訳だから、左右に絶対に避けたいハザードや OB ラインがある場合などに どこを狙って ショットをすべきかの判断が よりスマートに出来るようになる理屈だ。ショットが多少(1.8ヤード)右に出る傾向があること、そして、そこから 95% の確率で 14.4ヤード以上左右には ブレないことが分かっていれば、それを基準に保険を掛けたり、リスクを取れば良いのである。勿論、ここで得た飛距離のデータも 利用の仕方次第で 価値あるデータになるはずだ。
もし、自分の ドライバー、スプーン、5I - 7I - 9I、AW のショットの能力に関して 前述のようなデータがあったら どうだろう。多分に 今までのコース・マネジメントの仕方とは違ってくるだろうし、不安感も少なくなるはずだ。機会を見て、自分のデータを練習場で取ってみることを オススメしたい。当然、コースでは(ライや風の影響など)練習場とは異なった環境でプレーをする訳だから 練習場で採取したデータだけに頼るのは危険だが 自分なりに そうしたことも勘案し、σ の考え方を取り入れたコース・マネジメントについて研究して欲しいものである。そんなことで、以下は 統計学の基礎知識と題した σ に関する補足説明である。
♦ 統計学(Stats) の基礎知識
統計学は バラつき (variability) に係わる学問である。自然界の様々な事象を区別したり、場合によっては、予測する根拠を提供したり出来るもので、幅広い分野で応用されている。予測と言えば 確率論が より馴染みのある学問であるが、確率論は 統計学的に処理されたデータを記述する際のツールとして使われるものである。
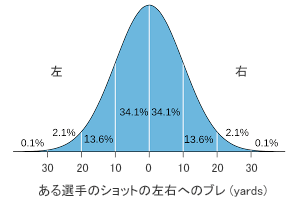 自然界の様々な事象をデータとして捉えると、その多くが 所謂 正規分布であることが知られている。正規分布 (normal distribution) は 右のグラフのように 中央が高く、両側に向かってだんだん低くなり 左右対称の釣鐘型になるが、この中央の一番高い位置が平均値になる。
自然界の様々な事象をデータとして捉えると、その多くが 所謂 正規分布であることが知られている。正規分布 (normal distribution) は 右のグラフのように 中央が高く、両側に向かってだんだん低くなり 左右対称の釣鐘型になるが、この中央の一番高い位置が平均値になる。
この分布のバラつきの度合いを示すものが標準偏差 (standar diviation) で、通常、シグマ (σ) の記号で表記される。グラフは ある選手のショットのバラつきの分布を示したものであるが、σ = 10( yards) の分布で 68.2% のショットが ±10-yard の範囲に入るということになる。極めて 重要な法則で コースマネジメントに有用な知識になるが、正規分布の場合、平均値 ±1σ に 68.2%、±2σ に 95.4%、そして、±3σ には 99.8% のデータが入るのである。この知識を 是非 コース・マネジメントに役立てて下さい。



